La guitare acoustique

Position des frettes : théorie

Nous allons désormais nous intéresser plus particulièrement à notre problématique,

c'est-à-dire nous demander pourquoi la note change lorsque nous plaquons la corde à tel ou tel endroit

du manche, ou en utilisant telle ou telle corde.

Avant tout, si vous ne comprenez pas les notions d’harmoniques et de fondamentales,

Nous savons que la fondamentale d’une corde vibrante est d’une fréquence calculable

grâce à cette formule :

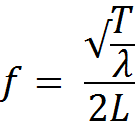
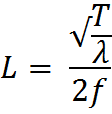
f	Fréquence de la note produite (Hertz)
L	Longueur de la section vibrante de la de corde (m)

T	Tension exercée par les mécaniques sur la corde (Newton)
λ	Masse linéique de la corde (g/m)

Nous vérifions alors la crédibilité de cette formule.

Selon elle, lorsque la longueur L diminuerait, la fréquence f augmenterait, ce qui est juste

(nous avons brièvement réalisé l’expérience, même si cela parait logique à la plupart des gens).

Ensuite, lorsque la tension T (accordage des cordes) augmente, la fréquence augmente également :

ceci est également juste (plus on tend une corde, plus le son qu’elle produit est aigu).

Et pour finir, plus la masse linéique serait élevée, plus la fréquence serait basse : une fois de plus correct.

En effet, plus une corde est lourde (donc épaisse), plus le son produit est grave ; c’est pourquoi il existe

différents tirants de corde.

Avant tout, nous remarquons que le numérateur ne dépend que de paramètres étant en rapport

avec la nature de la corde en elle-même (nous étudierons la tension et la masse linéique dans la partie suivante).

Nous essayons alors de nous familiariser avec notre formule, et obtenons ceci rapidement :

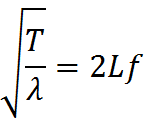
En pinçant une corde à vide de longueur L’ (= 64,2 cm, pour une guitare),

nous pouvons ainsi déterminer cette constante facilement, connaissant la fréquence de la note alors jouée (notée f’).

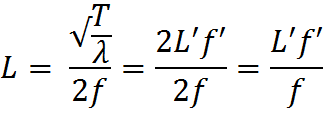
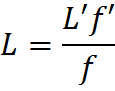
f	Fréquence de la note désirée
f’	Fréquence de la corde à vide

L	Longueur de la section de corde vibrante (= position des frettes)
L’	Longueur de la corde à vide (= 642 mm pour une guitare)

Voici la fréquence des notes normalement produites par les cordes de la guitare,

jouées à vide :

A partir de ceci, et connaissant la formule donnant

la fréquence d’une note de musique, nous obtenons cela :

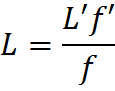
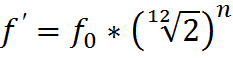
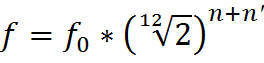
f₀	Fréquence de la note de référence (440 Hz)
n	Différence de demi-tons entre la note à vide et f₀

n’	Différence de demi-tons entre la note à vide et la note désirée
L	Longueur de la section de corde vibrante, ou distance entre la frette et le chevalet

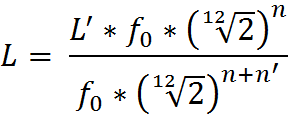
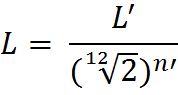
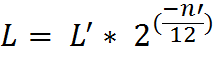
En utilisant cette formule, nous pouvons ainsi déterminer la position des frettes sur le manche de la guitare :

Exemple pour la 3^e frette, puis calcul de toutes :

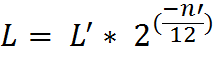
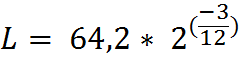
De la même façon, nous pouvons calculer la position de chaque frette, de façon théorique :

(valeurs exprimées en centimètres)

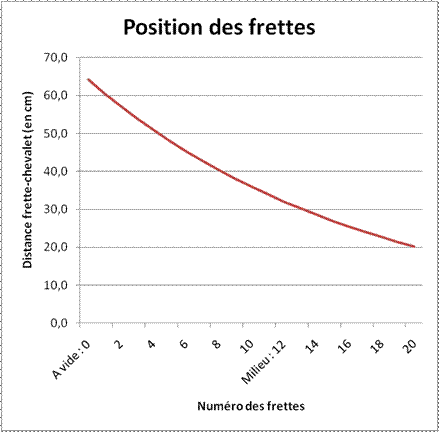
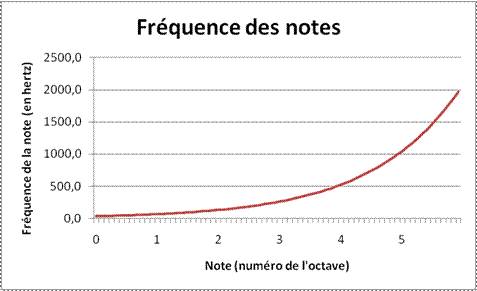
Nous remarquons que les frettes sont de plus en plus rapprochées lorsque les notes montent vers l’aigu :

la courbe de la position des frettes est exponentielle. En effet, cela est dû au fait que la fonction

donnant la fréquence des notes croît également de cette façon.

guitare-classique-etude-enfant-2

Site créé dans le cadre des TPE 2009-10 par

Matthias Lemainque, Lucas Prost & Romain Eliasse.